Năm 2012

(Nội dung chủ yếu được dịch từ trang Webhttps://www.nobelprize.org/prizes/economic-sciences/2012/popular-information/ )

Giải Nobel Kinh tế 2012

Giải thưởng Sveriges Riksbank về Khoa học Kinh tế tưởng nhớ Alfred Nobel năm 2012 được trao chung cho Alvin E. Roth và Lloyd S. Shapley

“vì lý thuyết về các phân bổ ổn định và việc áp dụng lý thuyết này trong thiết kế thị trường.”

"for the theory of stable allocations and the practice of market design"

Những người đoạt giải

Alvin E. Roth

Alvin E. Roth là nhà kinh tế học người Mỹ, sinh ngày 18 tháng 12 năm 1951 tại New York (Hoa Kỳ). Alvin Roth theo học tại Đại học Columbia, sau đó tiếp tục nghiên cứu và nhận bằng Tiến sĩ tại Đại học Stanford vào năm 1974. Trong sự nghiệp học thuật của mình, ông từng giảng dạy và nghiên cứu tại Đại học Illinois, Đại học Pittsburgh, và từ năm 1998 gia nhập Đại học Harvard, đồng thời công tác tại Harvard Business School. Năm 2012, ông quay trở lại Stanford. Alvin Roth đã lập gia đình và có hai người con.

Đóng góp học thuật quan trọng nhất của Alvin Roth nằm ở lĩnh vực thiết kế thị trường (market design) – một nhánh của kinh tế học nghiên cứu cách xây dựng các quy tắc và cơ chế để kết nối hiệu quả các bên tham gia thị trường. Trong khi Lloyd Shapley tập trung phát triển lý thuyết ghép cặp (matching theory) từ góc độ toán học, thì Alvin Roth đã đưa các kết quả lý thuyết này vào thực tiễn, bắt đầu từ những năm 1980.

Thông qua các nghiên cứu thực nghiệm và thí nghiệm trong phòng thí nghiệm, Roth chỉ ra rằng tính ổn định là yếu tố then chốt quyết định sự thành công của các cơ chế ghép cặp. Một cơ chế được xem là ổn định khi không tồn tại cặp tác nhân nào có động cơ rời bỏ cơ chế để tự ghép với nhau. Nếu thiếu tính ổn định, thị trường dễ bị phá vỡ bởi các thỏa thuận ngoài luồng.

Dựa trên những hiểu biết này, Alvin Roth đã thiết kế và cải tiến nhiều hệ thống ghép cặp quan trọng trong đời sống, tiêu biểu như: phân bổ bác sĩ nội trú cho bệnh viện, xếp học sinh vào trường học, và kết nối người hiến tạng với bệnh nhân cần ghép. Các cơ chế này không chỉ nâng cao hiệu quả phân bổ nguồn lực mà còn góp phần tăng công bằng và phúc lợi xã hội.

Với những đóng góp vừa mang tính lý thuyết sâu sắc vừa có giá trị ứng dụng rộng lớn, Alvin E. Roth được xem là một trong những nhà kinh tế tiêu biểu đã thu hẹp khoảng cách giữa kinh tế học trừu tượng và các vấn đề thực tiễn của xã hội hiện đại.

Lloyd S. Shapley

Lloyd S. Shapley là nhà toán học và kinh tế học người Mỹ, sinh ngày 2 tháng 6 năm 1923 tại Cambridge, Massachusetts, và qua đời ngày 12 tháng 3 năm 2016 tại Tucson, Arizona.

Lloyd Shapley lớn lên tại Cambridge trong một gia đình trí thức; cha ông là một nhà thiên văn học. Ông theo học toán học tại Đại học Harvard, nhưng quá trình học tập bị gián đoạn do ông phục vụ trong quân đội Hoa Kỳ trong Thế chiến thứ hai. Sau chiến tranh, Shapley làm việc một thời gian tại Tổ chức nghiên cứu RAND ở Santa Monica, California, trước khi nhận bằng Tiến sĩ tại Đại học Princeton. Năm 1954, ông quay trở lại RAND và làm việc tại đây cho đến năm 1981, khi ông được bổ nhiệm làm giáo sư tại Đại học California, Los Angeles (UCLA). Lloyd Shapley đã lập gia đình và có hai người con.

Đóng góp khoa học cốt lõi của Lloyd Shapley nằm ở việc ứng dụng lý thuyết trò chơi hợp tác (Cooperative Game Theory) để nghiên cứu các cơ chế ghép cặp (matching). Từ những năm 1960, ông đã tập trung vào một câu hỏi nền tảng của kinh tế học: làm thế nào để ghép nối các tác nhân khác nhau theo cách tốt nhất có thể.

Trong khuôn khổ lý thuyết này, tính ổn định là yếu tố then chốt. Một phân bổ ổn định là phân bổ mà không tồn tại hai tác nhân nào muốn rời bỏ sự sắp xếp hiện tại để ghép cặp với nhau, bởi vì cả hai đều thấy phương án đó tốt hơn. Nếu thiếu tính ổn định, các cơ chế phân bổ rất dễ bị phá vỡ bởi những thỏa thuận ngoài luồng.

Cùng với các cộng sự, Lloyd Shapley đã xác định và chứng minh sự tồn tại của những cơ chế ghép cặp đạt được tính ổn định, đặt nền móng lý thuyết cho nhiều ứng dụng thực tiễn sau này. Các kết quả của ông đã trở thành cơ sở toán học và kinh tế học vững chắc cho lĩnh vực thiết kế thị trường, mà Alvin Roth là người phát triển mạnh mẽ về mặt ứng dụng.

Với những đóng góp mang tính nền tảng, lâu dài và có ảnh hưởng sâu rộng, Lloyd S. Shapley được xem là một trong những học giả quan trọng nhất của thế kỷ XX trong lĩnh vực lý thuyết trò chơi và kinh tế học hiện đại.

Nội dung nghiên cứu của giải Nobel Kinh tế 2012.

Phân tích kinh tế truyền thống nghiên cứu các thị trường trong đó giá cả điều chỉnh để cung bằng cầu. Cả lý thuyết lẫn thực tiễn đều cho thấy thị trường vận hành tốt trong nhiều trường hợp. Tuy nhiên, trong một số tình huống, cơ chế thị trường tiêu chuẩn gặp phải vấn đề, và có những trường hợp giá cả hoàn toàn không thể được sử dụng để phân bổ nguồn lực.

Chẳng hạn, nhiều trường học và đại học không được phép thu học phí, và trong trường hợp cấy ghép nội tạng, việc thanh toán bằng tiền bị loại trừ vì các lý do đạo đức. Tuy vậy, trong những trường hợp này – cũng như trong nhiều tình huống khác – việc phân bổ vẫn phải được thực hiện. Vậy những quá trình phân bổ như vậy thực sự diễn ra như thế nào, và khi nào thì kết quả đạt được là hiệu quả?

Lý thuyết ghép cặp - Matching theory

Thuật toán Gale–Shapley

Phân tích các cơ chế phân bổ dựa trên một ý tưởng khá trừu tượng. Nếu những con người duy lý (rational people) – hiểu rõ lợi ích tốt nhất của mình và hành động phù hợp với điều đó – tự do tham gia trao đổi lẫn nhau không bị hạn chế, thì kết quả thu được sẽ là hiệu quả. Nếu không hiệu quả, một số cá nhân sẽ tìm cách thiết lập các giao dịch mới để cải thiện lợi ích của bản thân. Một phân bổ mà tại đó không cá nhân nào nhận thấy có thể thu được lợi ích từ các trao đổi tiếp theo được gọi là ổn định.

Khái niệm tính ổn định (stability) là một khái niệm trung tâm của lý thuyết trò chơi hợp tác (cooperative game theory) – một lĩnh vực trừu tượng của kinh tế học toán học nhằm xác định cách mà mọi cấu hình của các cá nhân duy lý có thể cùng nhau lựa chọn một phương án phân bổ. Người kiến tạo chủ yếu của nhánh lý thuyết trò chơi này là Lloyd Shapley, người đã phát triển các khái niệm cốt lõi của nó trong những năm 1950 và 1960.

Trao đổi không bị hạn chế (Unrestricted trading ) là một giả định then chốt làm nền tảng cho khái niệm ổn định. Mặc dù giả định này giúp cho việc phân tích trở nên rõ ràng, nhưng rất khó hình dung trong nhiều tình huống thực tế. Năm 1962, Shapley đã áp dụng ý tưởng về tính ổn định vào một trường hợp đặc biệt. Trong một bài báo ngắn viết chung với David Gale, ông đã xem xét bài toán ghép cặp theo cặp: làm thế nào để ghép các cá nhân thành từng cặp khi mỗi người có những quan điểm khác nhau về ai là đối tác ghép cặp tốt nhất.

Ghép cặp đối tác

Gale và Shapley đã phân tích bài toán ghép cặp ở một mức độ trừu tượng và tổng quát. Họ sử dụng hôn nhân như một ví dụ minh họa. Làm thế nào để ghép mười phụ nữ với mười đàn ông, trong khi vẫn tôn trọng các sở thích cá nhân của mỗi người? Thách thức chính là thiết kế một cơ chế đơn giản có thể dẫn đến một sự ghép cặp ổn định, trong đó không có cặp nào muốn chia tay để hình thành một cặp mới mang lại lợi ích cao hơn cho cả hai bên.

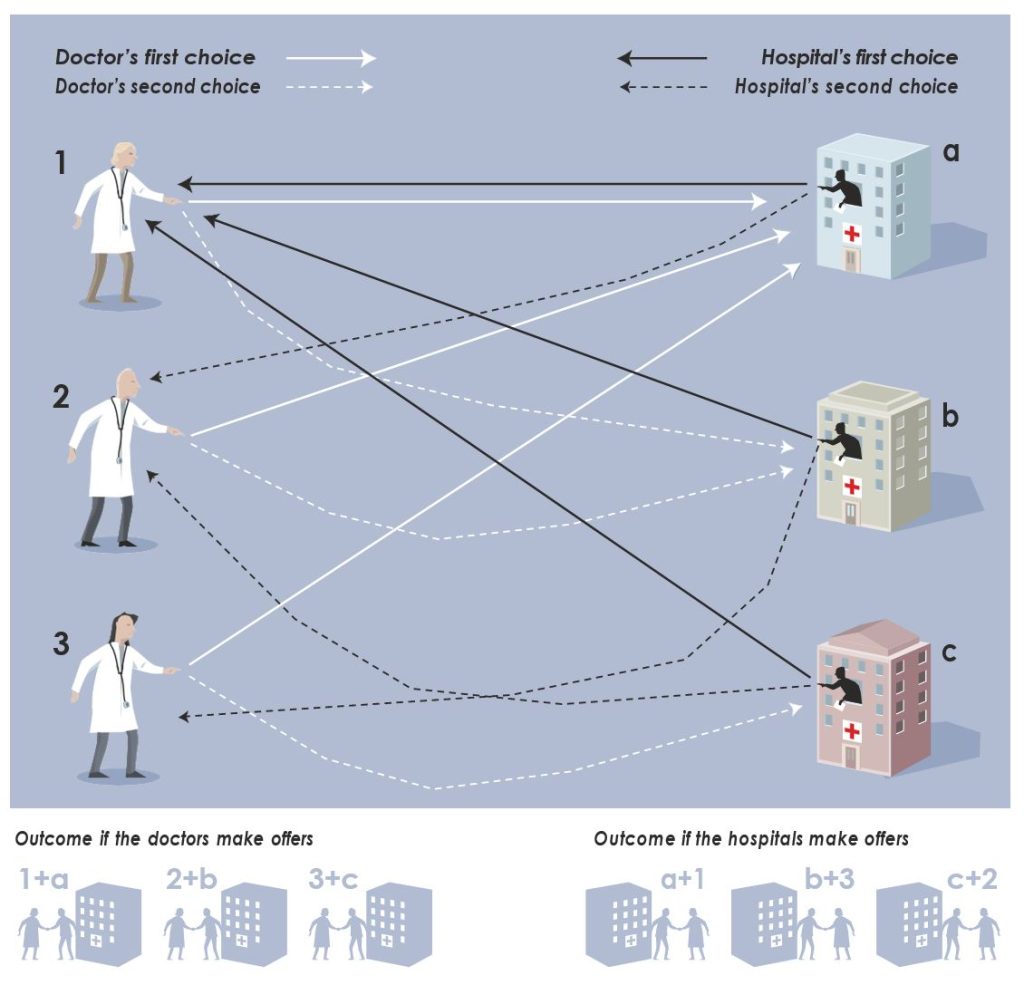
Lời giải – thuật toán “chấp nhận trì hoãn” (deferred acceptance) của Gale–Shapley – là một tập hợp các quy tắc đơn giản nhưng luôn trực tiếp dẫn đến một ghép cặp ổn định.

Thuật toán Gale–Shapley có thể được thiết lập theo hai cách đối xứng: hoặc nam giới đề xuất với nữ giới, hoặc nữ giới đề xuất với nam giới. Trong trường hợp thứ hai, quá trình bắt đầu khi mỗi người phụ nữ đề xuất với người đàn ông mà cô thích nhất. Mỗi người đàn ông sau đó xem xét các đề xuất mà mình nhận được (nếu có), giữ lại đề xuất mà anh ta cho là hấp dẫn nhất (nhưng chưa chấp nhận ngay) và từ chối các đề xuất còn lại. Những người phụ nữ bị từ chối ở vòng đầu tiên sẽ tiếp tục đề xuất với lựa chọn tốt thứ hai của mình, trong khi các người đàn ông một lần nữa giữ lại đề xuất tốt nhất và từ chối phần còn lại. Quá trình này tiếp diễn cho đến khi không còn người phụ nữ nào muốn đưa ra đề xuất mới. Khi đó, mỗi người đàn ông chấp nhận đề xuất mà mình đang giữ, và quá trình kết thúc. Gale và Shapley đã chứng minh bằng toán học rằng thuật toán này luôn dẫn đến một ghép cặp ổn định.

Cách thiết lập cụ thể của thuật toán có những hệ quả phân phối rất quan trọng; việc ai là người có quyền đề xuất – phụ nữ hay đàn ông – có ý nghĩa rất lớn. Nếu phụ nữ là người đề xuất, kết quả sẽ tốt hơn cho họ so với trường hợp đàn ông đề xuất, bởi vì một số phụ nữ sẽ ghép được với người đàn ông mà họ thích hơn, và không người phụ nữ nào rơi vào tình trạng tệ hơn so với khi đàn ông có quyền đề xuất. Thậm chí, kết quả này là phương án ghép cặp ổn định tốt nhất có thể đối với phụ nữ. Ngược lại, thuật toán đảo chiều – nơi đàn ông là người đề xuất – sẽ dẫn đến kết quả tệ nhất từ góc nhìn của phụ nữ.

Sự rõ ràng và thanh nhã của bài báo Gale–Shapley đã khiến nó sớm được đưa vào danh mục tài liệu học tập của sinh viên kinh tế trên toàn thế giới. Tuy nhiên, ý nghĩa thực tiễn của công trình này chỉ được nhận ra muộn hơn. Vào đầu những năm 1980, Alvin Roth bắt đầu nghiên cứu một bài toán phân bổ rất thực tế: thị trường dành cho các bác sĩ mới tốt nghiệp.

Bằng chứng thực nghiệm

Thị trường dành cho bác sĩ mới tốt nghiệp

Tại Hoa Kỳ, sinh viên sau khi tốt nghiệp trường y thường được tuyển dụng làm bác sĩ nội trú (resident/intern) tại các bệnh viện, nơi họ chiếm một phần quan trọng của lực lượng lao động. Vào đầu thế kỷ XX, thị trường này phần lớn mang tính phi tập trung. Trong những năm 1940, sự cạnh tranh để thu hút số lượng sinh viên y khoa khan hiếm đã buộc các bệnh viện phải đưa ra các lời mời thực tập ngày càng sớm, đôi khi trước khi sinh viên tốt nghiệp vài năm. Các ghép cặp được hình thành trước khi sinh viên có thể chứng minh năng lực chuyên môn, thậm chí trước khi họ biết mình muốn theo đuổi chuyên ngành y nào. Khi một lời mời bị từ chối, thường đã quá muộn để bệnh viện đưa ra lời mời cho các ứng viên khác.

Một thị trường đầy rẫy những vấn đề như vậy không thể tạo ra các ghép cặp ổn định, bởi vì không đủ số lượng lời mời được đưa ra kịp thời để đảm bảo các giao dịch mang lại lợi ích cho cả hai bên. Để có thể đưa ra nhiều lời mời nhanh hơn, các bệnh viện đã áp đặt thời hạn rất nghiêm ngặt đối với việc phản hồi các lời mời. Điều này lại buộc sinh viên phải đưa ra quyết định sớm, khi họ chưa biết những cơ hội khác có thể xuất hiện sau đó.

Trước những vấn đề này, một cơ chế tập trung, gọi là Chương trình Ghép cặp Bác sĩ Nội trú Quốc gia (National Resident Matching Program – NRMP), đã được thiết lập vào đầu những năm 1950. Trong một bài báo năm 1984, Alvin Roth đã nghiên cứu thuật toán được sử dụng trong cơ chế này và phát hiện rằng nó có mối liên hệ chặt chẽ với thuật toán Gale–Shapley. Từ đó, ông đưa ra giả thuyết rằng nguyên nhân cốt lõi dẫn đến thành công của NRMP chính là việc nó tạo ra các ghép cặp ổn định.

Đến đầu những năm 1990, Roth tiếp tục nghiên cứu các thị trường y tế tương tự tại Vương quốc Anh. Tại đây, ông phát hiện rằng các vùng khác nhau áp dụng các thuật toán khác nhau: một số tạo ra ghép cặp ổn định, trong khi số khác thì không. Những cơ chế dẫn đến ghép cặp ổn định đã hoạt động hiệu quả, trong khi các thuật toán còn lại đã sụp đổ theo nhiều cách khác nhau.

Thiết kế trong thực tiễn

Ghép cặp bác sĩ và bệnh viện

Mặc dù đạt được thành công đáng kể, NRMP vẫn gặp phải một số vấn đề. Số lượng nữ sinh viên y khoa ngày càng tăng, và ngày càng phổ biến các cặp đôi đều là bác sĩ mong muốn tìm vị trí thực tập tại cùng một khu vực. NRMP không thể đáp ứng những yêu cầu này, khiến nhiều ứng viên lựa chọn không tham gia cơ chế, một dấu hiệu cho thấy cơ chế đó không còn ổn định.

NRMP – nơi các bệnh viện là bên đưa ra đề xuất cho sinh viên – cũng bị chỉ trích vì có xu hướng ưu ái bệnh viện hơn sinh viên. Thật vậy, như Gale và Shapley đã chứng minh về mặt lý thuyết, bên đưa ra đề xuất trong một thị trường ghép cặp luôn có lợi thế một cách hệ thống; trong trường hợp này, các bệnh viện là bên được ưu ái.

Năm 1995, Alvin Roth được mời hỗ trợ thiết kế một thuật toán cải tiến nhằm khắc phục những vấn đề trên. Cùng với Elliott Peranson, ông đã xây dựng một thuật toán mới, dựa trên việc ứng viên là bên đưa ra đề xuất và được thiết kế để đáp ứng nhu cầu của các cặp đôi. Thuật toán mới, được NRMP chính thức áp dụng vào năm 1997, đã hoạt động rất hiệu quả, và kể từ đó hơn 20.000 vị trí mỗi năm đã được ghép cặp thành công với các ứng viên.

Các nghiên cứu nền tảng cho thiết kế sửa đổi này đã thúc đẩy sự phát triển của lý thuyết mới. Người ta nhận thấy rằng các ứng viên có thể thao túng thuật toán ban đầu – bằng cách từ chối những lời mời mà họ thực sự ưa thích và giữ lại những lời mời kém hơn – nhằm đạt được kết quả có lợi hơn cho mình. Trong một loạt bài báo lý thuyết, Alvin Roth đã chỉ ra rằng việc trình bày sai lệch sở thích thực sự của bản thân có thể phục vụ lợi ích của bên nhận đề xuất (trong NRMP ban đầu là sinh viên) đối với một số thuật toán nhất định.

Dựa trên hiểu biết này, thuật toán NRMP sửa đổi đã được thiết kế sao cho miễn nhiễm với việc sinh viên khai báo sai sở thích. Hơn nữa, các mô phỏng bằng máy tính đã xác nhận rằng, trong thực tế, thuật toán này không nhạy cảm với các hành vi thao túng chiến lược từ phía các bệnh viện.

Ghép học sinh và trường trung học - Matching students and high-schools

Thuật toán Gale–Shapley đã chứng tỏ tính hữu ích trong nhiều ứng dụng khác, chẳng hạn như lựa chọn trường trung học. Trước năm 2003, các học sinh nộp đơn vào trường trung học công lập tại Thành phố New York được yêu cầu xếp hạng năm lựa chọn ưu tiên nhất của mình, sau đó các danh sách sở thích này được gửi tới các trường. Các trường sẽ quyết định nhận, từ chối hoặc đưa học sinh vào danh sách chờ. Quy trình này được lặp lại trong hai vòng tiếp theo, và những học sinh chưa được nhận vào trường nào sau vòng thứ ba sẽ được phân bổ thông qua một quy trình hành chính.

Tuy nhiên, cơ chế này không cho học sinh đủ cơ hội để liệt kê đầy đủ các sở thích, và các trường cũng không có đủ cơ hội để đưa ra lời mời. Kết quả là khoảng 30.000 học sinh mỗi năm bị xếp vào những trường mà các em không hề liệt kê trong danh sách ưu tiên. Hơn nữa, quy trình này còn khuyến khích việc khai báo sai sở thích. Do các trường có xu hướng nhận những học sinh xếp trường đó là lựa chọn số một, nên những học sinh ít có khả năng trúng tuyển vào trường mơ ước sẽ thấy có lợi hơn nếu xếp một lựa chọn “thực tế” hơn lên hàng đầu. Trong khi đó, những học sinh trung thực khai báo đúng sở thích của mình lại phải chịu kết quả kém hơn một cách không cần thiết.

Năm 2003, Alvin Roth và các cộng sự đã hỗ trợ thiết kế lại quy trình tuyển sinh này, dựa trên phiên bản thuật toán Gale–Shapley trong đó ứng viên là bên đưa ra đề xuất. Thuật toán mới đã chứng minh được tính hiệu quả cao, với số học sinh bị xếp vào các trường mà họ không hề mong muốn giảm tới 90%. Ngày nay, ngày càng nhiều khu vực đô thị tại Hoa Kỳ đang sử dụng các biến thể của thuật toán Gale–Shapley trong việc phân bổ học sinh vào trường học.

Ghép thận và bệnh nhân - Matching kidneys and patients

Các bối cảnh ghép cặp được mô tả cho đến nay thường liên quan đến hai phía đều đưa ra các quyết định chủ động. Tuy nhiên, trong thực tế có những tình huống mang tính một phía, theo đó một bên hoàn toàn thụ động. Một ví dụ điển hình là việc ghép thận và các cơ quan hiến tặng khác cho những bệnh nhân cần cấy ghép. Làm thế nào để thực hiện việc này một cách hiệu quả?

Vấn đề này đã được Shapley và các cộng sự nghiên cứu, một lần nữa dưới góc độ trừu tượng và dựa trên khái niệm tính ổn định. Thuật toán được đề xuất – gọi là chu trình trao đổi tối ưu (top trading cycle) – thực chất rất đơn giản. Thuật toán này dựa trên việc phân bổ ban đầu các đối tượng và sau đó thực hiện các hoán đổi. Một thách thức trong trường hợp các cơ quan của con người là không phải mọi cặp thận – bệnh nhân đều tương thích, và các hoán đổi đa phương phức tạp có thể tốn khá nhiều thời gian. Một lần nữa, sự kết hợp giữa lý thuyết và nghiên cứu thực nghiệm đã được sử dụng để so sánh các phiên bản khác nhau của cơ chế trao đổi tối ưu. Kết quả là, các chuỗi hiến thận ngày càng phức tạp hiện đã được áp dụng tại nhiều bang ở Hoa Kỳ.

Mở rộng sang các thị trường mới

Một đặc điểm nổi bật của các ví dụ nêu trên là giá cả không phải là một phần của quá trình. Việc thiếu vắng cơ chế giá trong thuật toán Gale–Shapley cơ bản có làm hạn chế khả năng áp dụng của nó hay không? Không hẳn như vậy. Shapley và các nhà nghiên cứu khác đã xem xét những mở rộng của mô hình gốc, trong đó giá cả (chẳng hạn như tiền lương trong thị trường bác sĩ) được đưa vào như một phần của các đề nghị. Các thuật toán có bao gồm yếu tố giá vận hành theo cách khá tương tự và tạo ra các kết quả ghép cặp ổn định với những đặc điểm nhìn chung giống nhau.

Trên thực tế, ghép cặp có giá có mối liên hệ chặt chẽ với đấu giá, nơi các đối tượng được ghép với người mua và giá cả đóng vai trò quyết định. Nghiên cứu liên hệ các thuật toán ghép cặp với đấu giá gần đây đã tạo ra nhiều kết quả lý thuyết thú vị, và những kết quả này dường như có thể áp dụng trong thực tiễn. Một ví dụ tiêu biểu là đấu giá trên internet, đặc biệt là các công cụ tìm kiếm đấu giá không gian quảng cáo cho các nhà quảng cáo. Các công ty trong lĩnh vực này đã hưởng lợi từ những hiểu biết cốt lõi của các thuật toán Gale–Shapley và đã mời những nhà kinh tế hàng đầu làm chuyên gia trong việc thiết kế các hình thức đấu giá mới.

Giải thưởng năm nay tôn vinh một lĩnh vực nghiên cứu đang phát triển mạnh mẽ, nơi lý thuyết, bằng chứng thực nghiệm và thiết kế cơ chế được sử dụng một cách tương tác. Lloyd Shapley và Alvin Roth làm việc độc lập với nhau, nhưng thành công của nghiên cứu của họ bắt nguồn từ sự kết hợp giữa các kết quả lý thuyết của Shapley và những hiểu biết của Roth về giá trị ứng dụng thực tiễn. Lĩnh vực này tiếp tục mở rộng và hứa hẹn nhiều triển vọng to lớn trong tương lai.

Tài liệu tham khảo và tài liệu đọc thêm

https://www.nobelprize.org/prizes/economic-sciences/2012/popular-information/
https://www.nobelprize.org/uploads/2018/06/advanced-economicsciences2012-1.pdf
Roth A. E. (2008) What have we learned from market design?, Economic Journal, 118: 285–310.
Moulin H. (1995) Cooperative Microeconomics. Princeton University Press.
Roth A. E. and Sotomayor M. (1990) Two-sided Matching: a Study in Game-theoretic Modeling and Analysis, Econometric Society Monograph Series, Cambridge University Press.
Gale, D. and L. S. Shapley (1962) College admissions and the stability of marriage, American Mathematical Monthly, 69: 9–15.
Serrano, R. (2009) Cooperative games: core and Shapley value, In: Encyclopedia of Complexity and Systems Science, Edited by R. Meyers. New York: Springer.