Năm 2003
(Nội dung chủ yếu được dịch từ trang Web https://www.nobelprize.org )
Giải Nobel Kinh tế 2003
Giải Sveriges Riksbank về Khoa học Kinh tế tưởng nhớ Alfred Nobel năm 2003 được trao đồng đều cho Robert F. Engle III “vì các phương pháp phân tích chuỗi thời gian kinh tế với phương sai biến thiên theo thời gian (ARCH)” và Clive W. J. Granger
“vì các phương pháp phân tích chuỗi thời gian kinh tế có xu hướng chung (đồng liên kết)”.
“for methods of analyzing economic time series with common trends (cointegration)”
Người đoạt giải
Robert F. Engle III

Robert F. Engle III sinh ngày 10 tháng 11 năm 1942 tại Syracuse, bang New York, Hoa Kỳ. Robert Engle lớn lên ở vùng ngoại ô thành phố Philadelphia. Ông theo học cao học tại Đại học Cornell, ban đầu nghiên cứu vật lý, nhưng sau đó nhận ra niềm đam mê thực sự của mình là kinh tế học và đã chuyển hướng sang lĩnh vực này. Ông nhận bằng Tiến sĩ năm 1969. Ngoài học thuật, Robert Engle yêu thích du lịch, đi bộ đường dài, trượt tuyết và đặc biệt là khiêu vũ trên băng.
Đóng góp khoa học quan trọng nhất của Robert Engle là việc phát triển các mô hình thống kê về biến động (volatility), phản ánh thực tế rằng giá cổ phiếu và nhiều biến số tài chính khác thường luân phiên giữa các giai đoạn biến động cao và biến động thấp. Các mô hình này được gọi chung là ARCH (Autoregressive Conditional Heteroskedasticity) và đã trở thành công cụ không thể thiếu trong lý thuyết và thực hành định giá chênh lệch (arbitrage pricing), cũng như trong quản trị rủi ro tài chính hiện đại.
Năm 1975, Robert Engle gia nhập đội ngũ giảng viên của Đại học California, nơi ông công tác cho đến khi nghỉ hưu vào năm 2003. Tại thời điểm được trao giải Nobel Kinh tế, ông đang làm việc tại Đại học New York (New York University), và hiện nay vẫn tiếp tục giảng dạy và nghiên cứu tại đây. Những đóng góp của ông đã để lại dấu ấn sâu sắc, kết nối chặt chẽ giữa lý thuyết kinh tế, thống kê và tài chính ứng dụng.
Clive W.J. Granger

Clive W. J. Granger sinh ngày 4 tháng 9 năm 1934 tại Swansea, Vương quốc Anh và qua đời ngày 27 tháng 5 năm 2009 tại San Diego, bang California, Hoa Kỳ. Khi mới sáu tuổi, trong bối cảnh cha ông tham gia Thế chiến thứ hai, gia đình ông chuyển đến Cambridge. Clive Granger theo học Đại học Nottingham, nơi ông lựa chọn nghiên cứu toán học và kinh tế học, và nhận bằng Tiến sĩ năm 1956. Năm 1974, ông trở thành giáo sư tại Đại học California, San Diego (UC San Diego), nơi ông gắn bó lâu dài trong sự nghiệp học thuật.
Trong suốt sự nghiệp của mình, Clive Granger đã viết nhiều cuốn sách quan trọng, bao quát các lĩnh vực như phân tích và dự báo chuỗi thời gian, lý thuyết thống kê và thống kê ứng dụng, có ảnh hưởng sâu rộng đến cả nghiên cứu hàn lâm lẫn thực hành kinh tế.
Đóng góp khoa học nổi bật nhất của ông xuất phát từ việc nhận ra rằng phần lớn các chuỗi thời gian kinh tế vĩ mô tuân theo xu hướng ngẫu nhiên (stochastic trend), khiến cho những cú sốc tạm thời—chẳng hạn đối với GDP—có thể để lại tác động kéo dài. Những chuỗi như vậy được gọi là không dừng (nonstationary). Clive Granger đã chỉ ra rằng việc áp dụng các phương pháp thống kê dành cho chuỗi dừng vào phân tích dữ liệu không dừng có thể dẫn đến kết quả hoàn toàn sai lệch. Trên cơ sở đó, ông phát triển các phương pháp mới để phân tích mối quan hệ giữa các biến kinh tế có xu hướng chung, chẳng hạn như giữa tài sản và tiêu dùng, hay giữa tỷ giá hối đoái và mức giá.
Những đóng góp của Clive W. J. Granger đã đặt nền móng cho lý thuyết đồng liên kết (cointegration), trở thành công cụ không thể thiếu trong kinh tế lượng hiện đại và có ảnh hưởng lâu dài đến nghiên cứu kinh tế vĩ mô, tài chính và hoạch định chính sách.
Nội dung nghiên cứu của giải Nobel Kinh tế 2003
Khi ước lượng các mối quan hệ, đưa ra dự báo và kiểm định các giả thuyết xuất phát từ lý thuyết kinh tế, các nhà nghiên cứu thường sử dụng dữ liệu dưới dạng chuỗi thời gian – tức là các dãy quan sát được sắp xếp theo trình tự thời gian – để nghiên cứu các biến số kinh tế vĩ mô. Chẳng hạn, mức tiêu dùng của một nền kinh tế có thể phụ thuộc vào tổng thu nhập từ lao động và tài sản, lãi suất thực, cơ cấu độ tuổi của dân số, v.v. Ví dụ đơn giản nhất thường gặp trong giáo trình cho một mối quan hệ như vậy là một biểu thức tĩnh, tuyến tính chỉ gồm hai biến:
\[ g_t = a + b x_t + e_t \]
Theo phương trình này, biến \(g_t\) (ví dụ, mức tiêu dùng trong quý \(t\)) phụ thuộc vào biến \(x_t\) (ví dụ, thu nhập trong cùng kỳ). Thành phần cuối cùng – sai số ngẫu nhiên \(e_t\) – biểu thị phần biến động của \(g_t\) mà mô hình không thể giải thích được.
Dựa trên các chuỗi thời gian của các biến \(g_t\) và \(x_t\), các tham số \(a\) và \(b\) có thể được ước lượng bằng các phương pháp thống kê (được gọi là phân tích hồi quy). Để rút ra những kết luận hợp lệ, các phương pháp này cần phải phù hợp với những đặc tính riêng của dữ liệu chuỗi thời gian.
Các nhà khoa học đoạt giải năm nay đã phát triển những phương pháp nắm bắt được hai đặc tính then chốt của nhiều chuỗi thời gian kinh tế, đó là tính không dừng (nonstationarity) và độ biến động thay đổi theo thời gian (time-varying volatility).
Tính không dừng, xu hướng chung và đồng liên kết
Nhiều chuỗi thời gian kinh tế vĩ mô mang tính không dừng: một biến số, chẳng hạn như GDP, vì vậy thường vận động theo một xu hướng dài hạn, trong đó các cú sốc tạm thời có thể ảnh hưởng đến mức độ dài hạn của biến đó. Trái ngược với các chuỗi thời gian dừng, các chuỗi không dừng không thể hiện xu hướng rõ ràng quay trở lại một giá trị cố định hay một xu hướng đã cho.
Hình 1 minh họa hai ví dụ về các chuỗi thời gian như vậy. Đường cong gấp khúc, với những biến động lớn trong ngắn hạn, thể hiện tỷ giá hối đoái giữa đồng yên Nhật và đô la Mỹ theo từng tháng kể từ năm 1970. Đường cong trơn hơn cho thấy mức giá tiêu dùng của Nhật Bản so với Hoa Kỳ trong cùng giai đoạn.
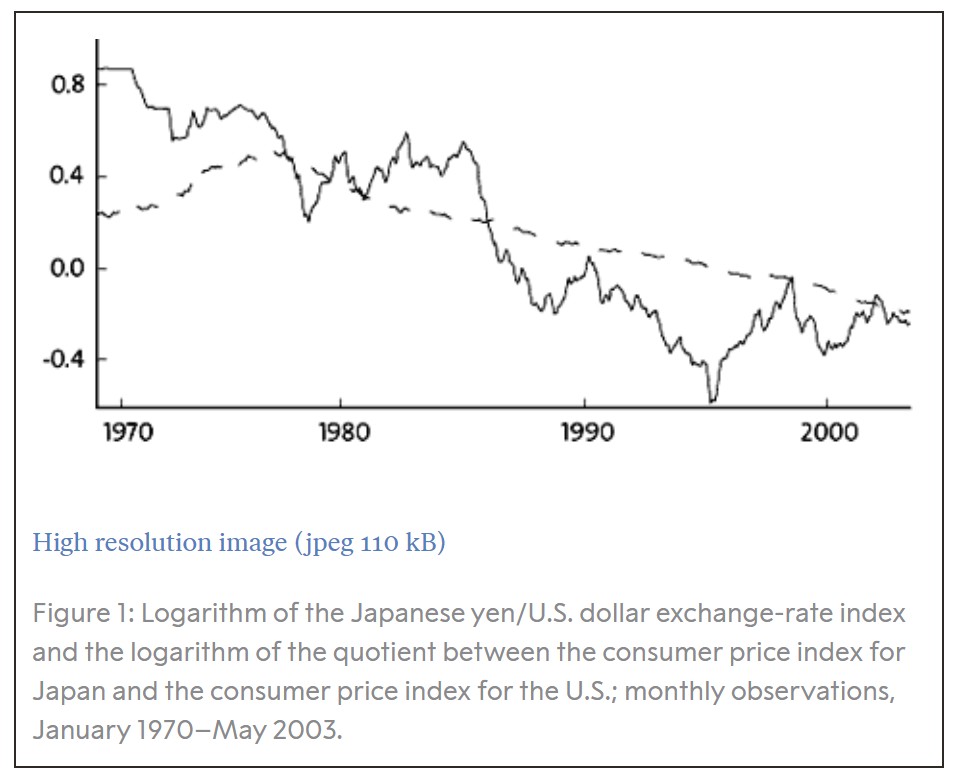
Trong một thời gian dài, mặc dù các chuỗi thời gian kinh tế vĩ mô thường mang tính không dừng, các nhà nghiên cứu chỉ có trong tay những phương pháp tiêu chuẩn vốn được phát triển cho dữ liệu dừng. Năm 1974, Clive Granger (cùng với cộng sự Paul Newbold) đã chỉ ra rằng việc ước lượng các mối quan hệ giữa các biến không dừng có thể dẫn đến những kết quả phi lý, khi các phương pháp thống kê sai lầm cho thấy tồn tại mối quan hệ có ý nghĩa thống kê giữa những biến hoàn toàn không liên quan với nhau. (Trong phương trình nêu trên, vấn đề phát sinh nếu sai số ngẫu nhiên \(e_t\) là không dừng. Khi đó, một kiểm định tiêu chuẩn có thể cho thấy hệ số \(b\) khác 0, mặc dù giá trị thực của nó bằng 0.)
Các cạm bẫy thống kê cũng có thể dẫn đến những kết quả gây hiểu lầm ngay cả trong những trường hợp mà mối quan hệ thực sự tồn tại. Cụ thể, rất khó phân biệt giữa các mối quan hệ tạm thời và lâu dài giữa các chuỗi thời gian không dừng. Ví dụ, lý thuyết kinh tế cho rằng trong dài hạn, một tỷ giá hối đoái mạnh hơn thường đi kèm với tốc độ tăng giá chậm hơn tương đối, bởi vì giá cả được biểu thị bằng cùng một đơn vị tiền tệ không thể chênh lệch quá lớn so với nhau. Khuynh hướng này cũng được thể hiện trong Hình 1, khi đồng yên tăng giá so với đô la Mỹ trong giai đoạn nghiên cứu, trong khi mức giá ở Hoa Kỳ lại tăng lên so với mức giá của Nhật Bản. Tuy nhiên, trong ngắn hạn, kỳ vọng và các dòng vốn có ảnh hưởng rất mạnh đến tỷ giá hối đoái, đến mức các phương pháp tiêu chuẩn có thể không đủ khả năng ước lượng chính xác mối quan hệ dài hạn.
Một cách tiếp cận phổ biến để xử lý vấn đề dữ liệu không dừng trước đây là xây dựng các mô hình thống kê dựa trên sai phân, tức là tốc độ tăng. Thay vì sử dụng tỷ giá hối đoái và mức giá tương đối, người ta sẽ ước lượng mối quan hệ giữa tỷ lệ mất giá của đồng tiền và lạm phát tương đối. Nếu các tốc độ tăng này thực sự là dừng, thì các phương pháp truyền thống sẽ cho ra kết quả hợp lệ. Tuy nhiên, ngay cả khi một mô hình thống kê chỉ dựa trên các sai phân có thể mô tả tốt động thái ngắn hạn của quá trình, thì nó lại cung cấp rất ít thông tin về sự đồng biến dài hạn giữa các biến. Điều này là một hạn chế đáng tiếc, bởi vì lý thuyết kinh tế thường được xây dựng trên các biến gốc (levels) chứ không phải trên các sai phân (differences).
Chính vì những đặc tính của dữ liệu không dừng, việc tìm ra các phương pháp có thể truy vết những mối quan hệ dài hạn tiềm ẩn phía sau “nhiễu” của các dao động ngắn hạn đã trở thành một thách thức lớn. Công trình của Clive Granger đã tạo ra một phương pháp luận như vậy cho phân tích thống kê
Đóng góp của Granger
Trong các công trình nghiên cứu được công bố trong thập niên 1980, Clive Granger đã phát triển những khái niệm và phương pháp phân tích kết hợp được góc nhìn ngắn hạn và dài hạn. Cốt lõi của các phương pháp này, cũng như của suy luận thống kê hợp lệ, nằm ở phát hiện của ông rằng một tổ hợp cụ thể của hai (hoặc nhiều) chuỗi không dừng có thể lại là chuỗi dừng. Lý thuyết kinh tế thường đưa ra chính những dự đoán như vậy: nếu tồn tại một mối quan hệ cân bằng giữa hai biến kinh tế, thì trong ngắn hạn chúng có thể lệch khỏi trạng thái cân bằng, nhưng về dài hạn sẽ điều chỉnh quay trở lại cân bằng. Chẳng hạn, lý thuyết truyền thống dự đoán sự tồn tại của tỷ giá hối đoái cân bằng dài hạn, trong đó mức giá được biểu thị bằng cùng một đơn vị tiền tệ sẽ ngang bằng với nhau. Granger đã đặt tên cho một tổ hợp dừng của các biến không dừng là đồng liên kết (cointegration).
Granger cũng chỉ ra rằng động học chung giữa các biến đồng liên kết có thể được biểu diễn bằng cái gọi là mô hình hiệu chỉnh sai số (error-correction model). Mô hình này không chỉ vững chắc về mặt thống kê mà còn mang ý nghĩa kinh tế rõ ràng. Ví dụ, động thái của tỷ giá hối đoái và mức giá được chi phối đồng thời bởi hai lực: (i) xu hướng làm “trơn” và thu hẹp các sai lệch so với tỷ giá cân bằng dài hạn, và (ii) các dao động ngắn hạn quanh quỹ đạo điều chỉnh hướng tới trạng thái cân bằng dài hạn đó.
Khái niệm đồng liên kết sẽ không thể trở nên hữu ích trong thực tiễn nếu thiếu các phương pháp thống kê mạnh mẽ để ước lượng và kiểm định giả thuyết. Clive Granger và Robert Engle đã giới thiệu những phương pháp như vậy trong một bài báo có ảnh hưởng đặc biệt lớn được công bố năm 1987. Trong đó, hai ông trình bày một kiểm định giả thuyết cho rằng một tập hợp các biến không dừng không đồng liên kết, đồng thời đề xuất phương pháp hai bước để ước lượng mô hình hiệu chỉnh sai số. Những phương pháp cải tiến hơn, hiện nay đã trở thành tiêu chuẩn, sau đó được phát triển bởi Søren Johansen.
Trong các nghiên cứu tiếp theo và thông qua hợp tác với những nhà khoa học khác, Granger đã mở rộng phân tích đồng liên kết theo nhiều hướng, bao gồm khả năng xử lý các chuỗi có tính mùa vụ (đồng liên kết theo mùa – seasonal cointegration) và các chuỗi mà quá trình điều chỉnh về cân bằng chỉ xảy ra khi độ lệch vượt quá một ngưỡng nhất định (đồng liên kết ngưỡng – threshold cointegration).
Ứng dụng
Công trình của Clive Granger đã làm thay đổi căn bản cách các nhà kinh tế xử lý dữ liệu chuỗi thời gian. Ngày nay, các kiểm định về tính dừng và đồng liên kết được thực hiện một cách thường xuyên như một bước nền tảng trong việc xây dựng các mô hình kinh tế lượng động. Phân tích đồng liên kết đặc biệt tỏ ra hữu ích trong những hệ thống mà động thái ngắn hạn chịu tác động của các nhiễu ngẫu nhiên lớn, trong khi các biến động dài hạn đồng thời bị ràng buộc bởi các mối quan hệ cân bằng kinh tế.
Một ví dụ điển hình là mối quan hệ giữa tỷ giá hối đoái và mức giá. Những ví dụ khác bao gồm mối quan hệ giữa tiêu dùng và tài sản (hai biến này phải nhất quán với nhau trong dài hạn, mặc dù trong ngắn hạn tiêu dùng biến động trơn hơn nhiều so với tài sản), giữa cổ tức và giá cổ phiếu (giá cổ phiếu trong dài hạn đi theo sự phát triển của cổ tức, nhưng trong ngắn hạn lại thể hiện các dao động lớn hơn đáng kể), và giữa lãi suất với các kỳ hạn khác nhau (trong đó lãi suất dài hạn và ngắn hạn được liên kết với nhau thông qua các kỳ vọng về lãi suất ngắn hạn trong tương lai, ngay cả khi trong ngắn hạn chúng có thể biến động theo những hướng khác nhau).
Độ biến động thay đổi theo thời gian và ARCH
Đánh giá rủi ro giữ vai trò trung tâm trong các hoạt động trên thị trường tài chính. Các nhà đầu tư so sánh lợi suất kỳ vọng của một tài sản với mức độ rủi ro của nó. Các ngân hàng và những tổ chức tài chính khác cũng cần đảm bảo rằng giá trị tài sản của họ không giảm xuống dưới một mức tối thiểu nào đó, vì nếu không sẽ có nguy cơ mất khả năng thanh toán. Những đánh giá như vậy không thể thực hiện nếu thiếu việc đo lường độ biến động của lợi suất tài sản. Robert Engle đã phát triển những phương pháp cải tiến để thực hiện các đánh giá loại này.
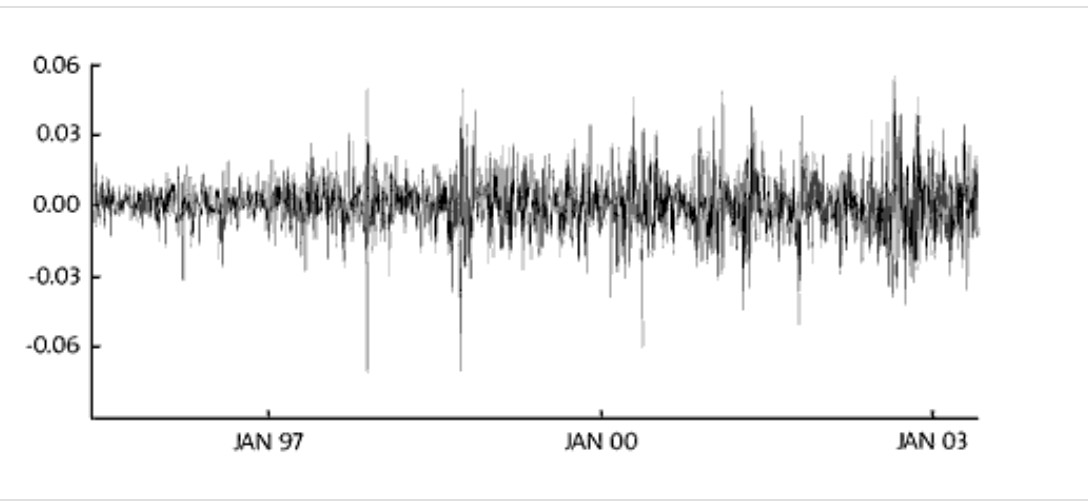
Hình 2 trình bày lợi suất của một khoản đầu tư vào chỉ số chứng khoán NYSE (Standard & Poor’s 500) trong tất cả các ngày giao dịch từ tháng 5 năm 1995 đến tháng 4 năm 2003. Lợi suất trung bình đạt 5,3% mỗi năm. Tuy nhiên, cũng có những ngày mà biến động giá (tăng hoặc giảm) vượt quá 5%. Độ lệch chuẩn của lợi suất ngày, tính trên toàn bộ giai đoạn, là 1,2%. Tuy vậy, khi quan sát kỹ hơn, có thể thấy rằng độ biến động không cố định theo thời gian: những thay đổi lớn (tăng hoặc giảm) thường được theo sau bởi những biến động lớn tiếp theo, trong khi những thay đổi nhỏ lại có xu hướng được theo sau bởi các dao động nhỏ.
Hiện tượng này được minh họa rõ ràng trong Hình 3, cho thấy độ lệch chuẩn (được tính trên bốn tuần gần nhất) thay đổi theo thời gian. Rõ ràng, độ lệch chuẩn biến thiên đáng kể, từ khoảng 0,5% trong những giai đoạn yên ả đến gần 3% trong các giai đoạn biến động mạnh hơn. Nhiều chuỗi thời gian tài chính khác cũng thể hiện đặc điểm tương tự về độ biến động thay đổi theo thời gian.
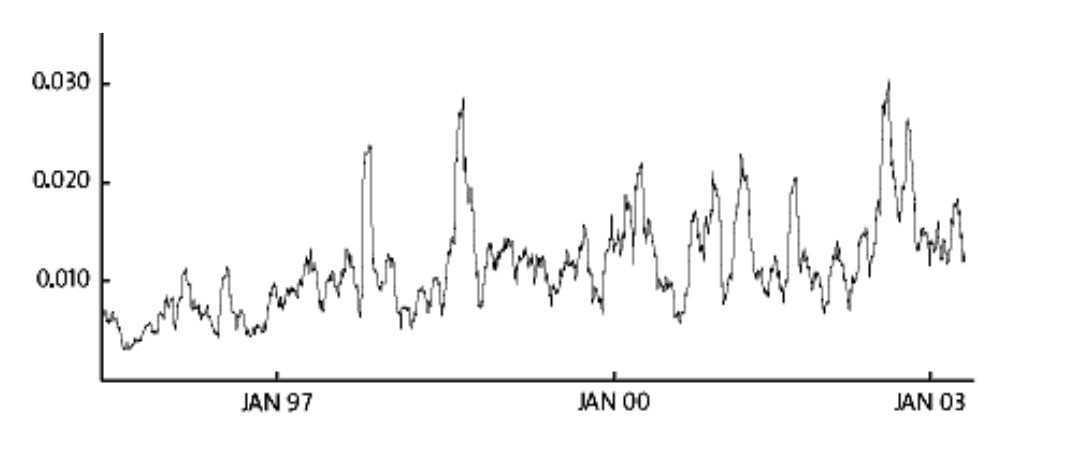
Đóng góp của Engle
Hình 3 cho thấy các phép tính hồi cứu về độ biến động thay đổi theo thời gian. Tuy nhiên, các nhà đầu tư và các tổ chức tài chính lại cần những đánh giá hướng tới tương lai – tức là dự báo – về độ biến động trong ngày, tuần hay năm tới. Trong một bài báo xuất sắc công bố năm 1982, Robert Engle đã xây dựng một mô hình cho phép thực hiện những đánh giá như vậy.
Các mô hình thống kê về lợi suất tài sản chỉ có thể giải thích được một phần biến động từ ngày này sang ngày khác. Phần lớn độ biến động vì thế được “chứa” trong thành phần sai số ngẫu nhiên (ký hiệu \(e_t\) trong phương trình mở đầu) – hay nói cách khác, trong sai số dự báo của mô hình. Trong các mô hình thống kê tiêu chuẩn, phương sai kỳ vọng của sai số ngẫu nhiên thường được giả định là không đổi theo thời gian. Rõ ràng, giả định này không phản ánh được những biến động lớn của lợi suất tài sản như được minh họa trong Hình 3.
Thay vào đó, Engle giả định rằng phương sai của sai số ngẫu nhiên trong một mô hình thống kê, tại một thời điểm nhất định, phụ thuộc một cách có hệ thống vào các sai số ngẫu nhiên đã xảy ra trước đó, sao cho các sai số lớn (nhỏ) có xu hướng được theo sau bởi các sai số lớn (nhỏ). Về mặt kỹ thuật, biến ngẫu nhiên này thể hiện phương sai có điều kiện thay đổi theo thời gian và có cấu trúc tự hồi quy (autoregressive conditional heteroskedasticity). Vì vậy, cách tiếp cận của ông được gọi tắt là ARCH.
Trong ví dụ của chúng ta, mô hình lúc này không chỉ bao gồm một phương trình dự báo lợi suất tài sản, mà còn có thêm một tập hợp các tham số mô tả cách phương sai của sai số ngẫu nhiên trong phương trình này phụ thuộc vào các sai số dự báo ở những giai đoạn trước. Engle đã chỉ ra cách ước lượng các mô hình ARCH và giới thiệu một kiểm định thực tiễn cho giả thuyết rằng phương sai có điều kiện của sai số ngẫu nhiên là không đổi.
Trong các nghiên cứu tiếp theo và thông qua hợp tác với các nghiên cứu sinh và đồng nghiệp, Engle đã phát triển khái niệm này theo nhiều hướng khác nhau. Phần mở rộng nổi tiếng nhất là mô hình ARCH tổng quát (GARCH) do Tim Bollerslev đề xuất năm 1986. Trong mô hình này, phương sai của sai số ngẫu nhiên tại một thời điểm không chỉ phụ thuộc vào các sai số trước đó, mà còn phụ thuộc vào chính phương sai của các giai đoạn trước. Sự phát triển này tỏ ra vô cùng hữu ích; GARCH hiện là mô hình được sử dụng phổ biến nhất trong thực tiễn phân tích độ biến động tài chính.
Ứng dụng của ARCH/GARCH
Trong bài báo đầu tiên về ARCH, Engle đã sử dụng mô hình độ biến động thay đổi theo thời gian để nghiên cứu lạm phát. Tuy nhiên, không lâu sau đó, người ta nhận ra rằng các ứng dụng quan trọng nhất của mô hình này nằm trong lĩnh vực tài chính, nơi các hoạt động chủ yếu nhằm quản lý và định giá các loại rủi ro khác nhau. Vì vậy, các mô hình định giá thể hiện mối quan hệ giữa giá chứng khoán và độ biến động: lợi suất kỳ vọng của một cổ phiếu cụ thể phụ thuộc vào hiệp phương sai giữa lợi suất của cổ phiếu đó và danh mục thị trường (theo CAPM do William Sharpe, người đoạt giải Nobel Kinh tế năm 1990, phát triển); giá quyền chọn phụ thuộc vào phương sai của lợi suất tài sản cơ sở (theo công thức Black–Scholes, được trao Giải Nobel Kinh tế năm 1997 cho Merton và Scholes), v.v.
Trong các nghiên cứu hợp tác với những nhà khoa học khác, Engle đã mô tả những mối quan hệ này bằng cách phát triển các mô hình GARCH-M, trong đó lợi suất kỳ vọng phụ thuộc vào các phương sai và hiệp phương sai thay đổi theo thời gian, và do đó bản thân lợi suất kỳ vọng cũng trở thành biến đổi theo thời gian.
Vậy, độ biến động thay đổi theo thời gian có ý nghĩa thực tiễn như thế nào? Nếu áp dụng một mô hình GARCH cho lợi suất cổ phiếu trong Hình 2, thì độ biến động có điều kiện, được biểu thị bằng độ lệch chuẩn, sẽ dao động trong khoảng từ 0,5% đến 3% trong giai đoạn đang xét. Nếu một nhà đầu tư nắm giữ một danh mục tương ứng với chỉ số Standard & Poor’s 500, thì người đó có thể chịu rủi ro mất bao nhiêu vốn trong ngày hôm sau? Với độ lệch chuẩn dự báo là 0,5%, khoản lỗ của nhà đầu tư đó – với xác suất 99% – sẽ không vượt quá 1,2% giá trị danh mục. Nếu độ lệch chuẩn dự báo là 3%, thì mức tổn thất vốn tương ứng có thể lên tới 6,7%.
Những phép tính tương tự về giá trị chịu rủi ro (Value at Risk – VaR) giữ vai trò then chốt trong phân tích rủi ro hiện đại, khi các ngân hàng và tổ chức tài chính khác đánh giá rủi ro thị trường của danh mục chứng khoán mà họ nắm giữ. Kể từ năm 1996, một thỏa thuận quốc tế (còn gọi là các quy tắc Basel) cũng quy định việc sử dụng Value at Risk trong việc kiểm soát yêu cầu vốn của các ngân hàng. Thông qua việc được áp dụng trong những bối cảnh này và nhiều bối cảnh khác, mô hình ARCH đã trở thành một công cụ không thể thiếu trong đánh giá rủi ro của khu vực tài chính.
Tài liệu tham khảo và tài liệu đọc thêm
- https://www.nobelprize.org/prizes/economic-sciences/2004/popular-information/
- https://www.nobelprize.org/prizes/economic-sciences/2004/advanced-information/
- Engle, R.F., “GARCH101: The Use of ARCH/GARCH Models in Applied Econometrics,” Journal of Economic Perspectives, Vol. 15, No. 4, Fall 2001, pp. 157–168.
- Poon, S-H., and C.W.J. Granger, “Forecasting Financial Market Volatility,” Journal of Economic Literature, Vol. 41, No. 2, June 2003, pp. 478–539.
- Granger, C.W.J., “Developments in the Study of Cointegrated Variables”, Oxford Bulletin of Economics and Statistics, Vol. 48, 1986, pp. 213–228.
- Murray, M.P., “A Drunk and her Dog: An Illustration of Cointegration and Error Correction”, The American Statistician, Vol. 48, No.1, Feb 1994, pp. 37–39.
- Phillips, P.C.B., “ET Interview: Clive Granger”, Econometric Theory, Vol. 13, 1997, pp. 253–304.